Bài toán lớn tiếp theo mà các nhà toán học đang cố gắng giải là gì?

Tính phức tạp, sự khả tính và Logic

Những câu hỏi khởi nguồn về cái gì có thể tính toán được và tính toán thế nào cho hiệu quả có sự liên quan mật thiết đến những câu hỏi về toán logic: những phương pháp chứng minh, kiểu mẫu và những giới hạn của sự nỗ lực nghiên cứu trong toán học. Thật vậy, theo tôi, một trong những câu hỏi quan trọng nhất ở đây là: Đâu sẽ là tương lai của toán học, bởi máy tính đã và đang tăng cường khả năng của chính chúng ta? Câu hỏi này sẽ được trả lời, theo cách này hay cách khác, trong vòng 100 năm tới.

Image result for Tính phức tạp, sự khả tính và Logic

Có một điều chắc chắn rằng ngày càng có nhiều bài toán nền tảng mà chúng ta phải đối mặt. Bài toán nổi tiếng nhất, không nghi ngờ gì nữa, là P vs NP, một trong những bài toán Thiên niên kỷ (và cũng là bài toán sâu sắc nhất, theo cách nhìn nhận nhỏ bé, tầm thường của tôi). Khác với cái bài toán là mẹ-của-các-bài-toán này, việc tạo nên một dấu ấn đáng kể trong cái sở thú đa thức gồm hệ thống nhiều cấp bậc và vô cùng phức tạp chính là "bài toán lớn tiếp theo" dành cho cả ngành công nghiệp các nhà tư tưởng, những người làm việc cùng những dãy số đủ làm ta hoa mắt với các lớp/ cấp độ của tính phức tạp. Cụ thể mà nói, hiểu được những điểm nổi bật của việc tính toán lượng tử về cả mặt lý thuyết lẫn ứng dụng là nỗ lực quan trọng trong những thập kỷ tới.
Một trong những hướng đi (về lý thuyết) tạo ra nhiều sự tò mò nhất trong lĩnh vực nghiên cứu về sự khả tính, liệu pháp chứng minh và tính nền tảng là Thuyết về các loại phép Đồng luân (Homotopy Type Theory) và Nền tảng Đơn diệp (Univalent Foundations), sự phát triển của nó bị chậm lại một cách vô cùng đáng tiếc và đầy bi kịch do cái chết không báo trước, vào tháng 9 năm 2017, của chủ nhân giải thưởng Fields - Vladimir Voevodsky.

Vladimir Voevodsky là, giữa muôn vàn những cái tên khác mà mọi người có thể gọi ông, một người bám sát theo chủ nghĩa trực giác, hoặc ít nhất là ông bị hấp dẫn bởi chủ nghĩa trực giác và chủ nghĩa hữu hạn và coi nó như là một nền tảng tiềm năng đối với các mặt của toán học. Cá nhân tôi tin rằng phương pháp và ý tưởng của chủ nghĩa hữu hạn sẽ đóng một vai trò quan trọng trong tương lai của toán học, không chỉ bởi chúng theo cách nào đó vượt trội hơn cả về mặt tinh thần và tâm lý, mà còn bởi chúng vô cùng thú vị.
Chúng ta đã học được rất nhiều về liệu pháp chứng minh, nhưng tôi nghĩ chúng ta mới chỉ lướt trên bề mặt của phương pháp chứng minh phức tạp. Điều gì sẽ xảy ra nếu
một phỏng đoán lý thuyết về số học sai, nhưng lại đúng ở một vài số vô cùng lớn, không thể tính được? Hay sẽ thế nào nếu một mệnh đề có thể chứng minh được trong hệ ZFC (Số đếm lớn), nhưng chứng minh ngắn nhất cũng cực kì nhiều kí tự? (Nguyên văn: What if a statement is provable in ZFC, but the shortest proof is TREE(999) characters long? ).

Tôi tin rằng sự phá bỏ những giới hạn đẹp đẽ trong suy nghĩ về khả năng chứng minh của con người sẽ tiếp tục định nghĩa những mảnh ghép trọng tâm của toán học qua hàng thập kỉ, hay thế kỉ.
____________________

Chương trình Langlands
Image result for langlands

Robert Langlands là một người có tầm nhìn sâu trông rộng đủ để tạo nên toàn bộ một chương trình, thứ đã dẫn lối cuộc đời của rất nhiều người từ cuối những năm 60 và tránh xa được sự mất động lực. Chương trình Langlands đã được gọi là "Thuyết thống nhất danh giá của Toán học" bởi Edward Frenkel, và tôi nghĩ danh hiệu này chỉ hơi cường điệu một xíu. Nó là một chương trình táo bạo đến mức điên dồ, nó cũng khác thường ở chỗ nó không xuất hiện trong một số nguồn tôi đã đề cập đến ở trên.

Miêu tả chương trình này là một bài toán cực kì khó nhằn. Trong cuốn "Giới thiệu những điều cơ bản về Chương trình Langlands", Stephen Gelbart viết:
Ở đây có sự đan xen giữa sự vật lộn cực độ cũng như niềm say mê vô cùng của chương trình Langlands. Chỉ để đơn thuần phát biểu các phỏng đoán một cách chính xác thôi cũng đã đòi hỏi rất nhiều kiến thức về bộ máy hoạt động của lý thuyết số (class field theory), thuyết về cấu tạo của các nhóm đại số, thuyết về cách biểu diễn của nhóm số thực và số p-adic, và (ít nhất) một chút về ngôn ngữ hình học đại số. Nói cách khác, dù kết quả là rất hứa hẹn, quá trình khởi động cũng đã như muốn ngăn cấm chúng ta vậy.
Một cách vô cùng sửng sốt, Chương trình Langlands đề xuất rằng tất cả các chuỗi L, những đối tượng tối quan trọng trong lý thuyết số, "đến từ" sự biểu diễn của một số nhóm cụ thể nào đó. Nó tự động kết nối các dạng số, các thuyết adele(?) (adele ring), thuyết về sự biểu diễn số học cùng rất nhiều các thuyết liên quan khác về hình học, đại số, giải tích và lý thuyết số.
Chương trình Langlands không phải chỉ có một câu hỏi hay một phỏng đoán. Nó là cả một mạng lưới các ý tưởng. Chứng minh của Ngô Bảo Châu về "Bổ đề cơ sở" và chứng minh của Laurent Lafforgue về Quan hệ tương ứng Langlands trong phạm vi các phương trình là những thành tựu vĩ đại đã đem về cho họ giải thưởng Fields, nhưng họ chỉ mới nhích từng bước trong chương trình còn lớn hơn thế. Rất nhiều điều vẫn chưa được khám phá và hoàn thành, và tôi khá chắc là tiến trình của chương trình sẽ tiếp tục diễn ra trong những thập kỷ tới.
____________________

Những bức vẽ của trẻ con

Tôi biết nghe nó có vẻ hơi ngớ ngẩn một xíu, nhưng thực sự nó không vậy đâu. Ý tưởng về "dessins d’enfants" (tiếng Pháp, dịch: những bức vẽ của trẻ con) là một trong những di sản của Alexander Grothendieck, và tôi đồ rằng việc chứng minh, làm rõ ràng và xây dựng những ý tưởng của Grothendieck là một thách thức cực kì đáng được lưu tâm dành cho toán học.

Cụ thể, dessins d’enfants đề xuất một cách nhìn khác về một trong những đối tượng (mà theo quan điểm của tôi) bí ẩn và kì diệu nhất trong vũ trụ sâu rộng, chân thực này (thứ luôn trung lập với các xiềng xích của thế giới vật lý thật sự và ngẫu nhiên). Giá trị tuyệt đối của nhóm Galois Gal(-Q/Q) chắc là thứ kì lạ và lộng lẫy nhất trong tất cả. Bất cứ sự tiến triển nào có được để hiểu hơn về nhóm bí ẩn này - và sẽ có có tiến triển, tôi tin vậy - sẽ soi rọi ánh sáng vào câu hỏi sâu sắc nhất của lý thuyết số và hơn thế nữa. Ý tưởng của Grothendieck không phải là hướng đi duy nhất, nhưng là hướng đi đầy hứa hẹn và vô cùng thú vị, giống như phần lớn mọi thứ mà người đàn ông này phát hiện ra.
Một nội dung khác trong những ý tưởng của Grothendieck, những phạm trù cao cấp (higher categories) và thuyết tô-pô (topos theory), đã được theo đuổi bởi những con người phi thường và tận tâm, vĩ đại nhất có lẽ phải kể đến Jacob Lurie.

Tôi không nghĩ chúng ta có thể chắc rằng anh ấy sẽ hoàn thiện nó chỉ với một mình anh ấy, nhưng thật sự anh ấy là một người tài trí. Sẽ khó để dự đoán, nhưng có khả năng thuyết phạm trù cao cấp sẽ ngày càng lớn mạnh một cách đáng kể để nắm giữ vai trò tối quan trọng với tương lai toán học. Nhân tiện, nó cũng liên kết mật thiết tới một vài ý tưởng mà tôi đã nêu ra trong nội dung đầu tiên (Nền tảng Đơn diệp và vân vân).
____________________

Toán học trong Vật lý

Một trong 23 bài toán mơ hồ và khó hiểu nhất của Hilbert là Bài toán số 6. Nó được phát biểu như sau:
6. Nghiên cứu Toán học về các Tiên đề Vật lý. Các cuộc nghiên cứu về nền tảng của hình học đã đề xuất bài toán sau: "Coi như ở trong cùng một hạng mục, khi nói tới các tiên đề, ta thấy được những kiến thức khoa học vật lý mà các tiên đề toán học bao hàm đang đóng một vai trò quan trọng; nằm ở thứ hạng cao nhất phải kể đến lý thuyết về xắc suất và cơ học."

Hãy nhớ rằng: đây là năm 1900, có nghĩa là trước khi có Năm 1905 của Einstein, trước khi có Tính Tương đối chung, trước khi có Cơ học Lượng tử, trước khi có thuyết Vật mẫu Tiêu chuẩn và Trường Lượng tử và thuyết Đa dây. Hilbert đã không thể biết được các bạn đồng nghiệp ngành vật lý đã tiến được xa thế nào trong sự hiểu biết về vật lý, ông đã một mình tiên đề hóa nó. Và thách thức vẫn còn đó: để hình thành một mối liên kết chặt chẽ, các khuôn khổ toán học thống nhất cần miêu tả thế giới vật lý của chúng ta.
Từ sự nỗ lực khổng lồ này, Học viện Toán học Clay đã chọn ra một thử thách mang tính nền tảng hơn, nhưng vẫn vô cùng sâu sắc cho những Bài toán Thiên niên kỷ: Bài toán về sự thành lập thuyết Yang-Mills tương ứng với bất kỳ nhóm quy mô nào, và chỉ ra rằng nó có một lượng tối thiểu. Một cách khác để biểu diễn thử thách này trong một nội dung toán học, nó có thể là : tổ chức, tiên đề hóa và hiểu được các thuyết về trường lượng tử tô-pô.

Trong một nghiên cứu tuyệt vời miêu tả bài toán Yang-Mills, Jaffe và Witten viết:
...một bài toán chưa có một ví dụ toán học đầy đủ, cũng không có một định nghĩa chính xác về thuyết lượng tử tầm cỡ trong không thời gian bốn chiều. Liệu điều này sẽ thay đổi trong thế kỉ 21 chứ? Chúng tôi đều mong vậy!
Chắc chắn rằng, vật lý đối mặt thêm với rất nhiều những thử thách cùng với toán học. Một Bài toán Thiên niên kỷ khác tìm kiếm một chứng minh (hoặc một sự phủ nhận) rằng Những phương trình của Navier-Stokes thừa nhận một lời giải trơn tru chỉ được đưa ra nếu như nó ở trong điều kiện rào cản cũng cần phải trơn tru.

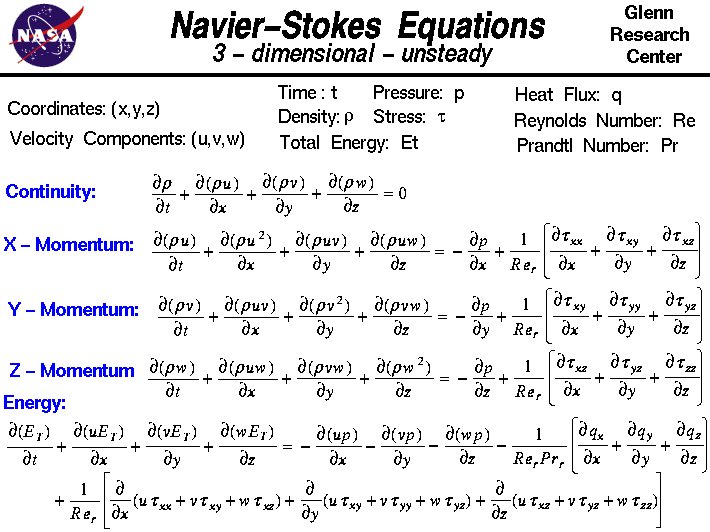
Đây là những phương trình nhiêu tả chuyển động dòng chảy; chúng không phải lượng tử hay dựa trên thuyết tương đối hay bất cứ gì giống vậy, nhưng chúng lại vô cùng thiết yếu đối với sựu hiểu biết của chúng ta về thế giới vĩ mô. Chúng cũng là ví dụ chìa khóa của những phương trình vi phân cục bộ không tuyến tính (PDEs - partial differential equations), và sự hiểu biết về chúng là một thách thức lớn và phải đối mặt nhiều khía cạnh của toán học. Chúng tôi thực thực sự mong muốn hiểu được chúng nếu, bất chấp đặc tính hỗn loạn tự nhiên, những phương trình này luôn có những lời giải trơn tru hay nếu chúng có thể "phá nhỏ ra" trong những điều kiện lý tưởng.
Cụ thể cho trường hợp Navier-Stokes, tôi nghĩ nhiều người chỉ đang đợi Terry Tao xử lý cái thứ cục cít đó luôn đi, mặc dù thực tế tính đến thời điểm hiện tại anh ấy đã trong tiến trình chỉ ra rằng tại sao bài toán này lại khó hơn mọi người nghĩ. Thật tình cờ, hướng làm của anh ấy đã hé lộ sự hình thành của những kiểu mẫu tính toán "cực kì mạnh mẽ" cùng với khung lõi của động lực chảy, mang đến cho chúng ta phạm vi của sự khả tính và chứng minh. Nếu lời giải của các phương trình vi phân cục bộ không tuyến tính đủ sức để phù hợp với logic bất thường, một vài bài toán nào đó trong các phương trình vi phân cục bộ không tuyến tính sẽ không thể giải được giống như một bài toán lủng củng.
Không cần biết là Tao hay bất kỳ ai tiến triển được lời giải của bài toán này cũng đều sẽ là một thành công lớn.
____________________

Giả thuyết (Suy rộng) Riemann

Một trong những ứng cử viên lớn khác cho "bài toán lớn tiếp theo" là Giả thuyết Riemann, Bài toán Thiên nien kỷ duy nhất vẫn còn nguyên vẹn kể từ khi danh sách của Hilbert ra đời năm 1900. Nó có thể không phải "bài toán lớn tiếp theo" sẽ được giải - có chúa mới biết nó mất bao lâu - nhưng nó chắc chắn sẽ tiếp tục bám lấy tâm trí, hy vọng và giấc mơ của nhân loại.

Giả thuyết Riemann nhìn có vẻ rất kỳ lạ: nó đề cập tới một phương trình cụ thể, Phương trình zeta Riemann S(s), và hỏi về vị trí của các nghiệm của nó (khác với những nhóm bài toán thông thường). Tất cả chúng đều được cho là nằm trong đường thưởng R(s) = 1/2.
Những phương trình cụ thể và nghiệm của chúng thường không phải là vấn đề dính dáng với vũ trụ, nhưng đây là một ngoại lệ vô cùng lớn. Phương trình zeta Riemann đóng vai trò tối quan trọng trong một vài lĩnh vực toán học (rõ ràng nhất là Lý thuyết Số). Hơn nữa, có một sự tổng quát rất tự nhiên trong Giả thuyết Riemann và những phương trình zeta khác, và thậm chí có nhiều ứng dụng ngoài tầm với hơn cả một mình Giả thuyết Riemann.

Bài toán này hiện đang đứng vững trong hơn 150 năm, và tôi không nghĩ rằng nó sẽ được giải trong thời gian ngắn đâu. Bất cứ khi nào có ai đó chứng minh được nó, hay thậm chí chỉ cần có sự tiến triển đáng kể trong hiểu biết về cái khó khăn ta mắc phải, đó sẽ là Bài toán lớn tiếp theo mà không cần phải bàn cãi.
____________________

Giả thuyết ABC

Từ khi được giới thiệu vào giữa những năm 80 thế kỷ trước, Giả thuyết ABC được biết đến với nhiệm vụ cung cấp một hướng đi thống nhất để hiểu rất nhiều bài toán cũ và mới trong Lý thuyết Số. Thực tế, nó bao hàm rất nhiều bài toán đạt giải Fields trong suốt 50 năm qua, và thường xuyên có các bài luận văn chỉ ra rằng nó liên quan đến bài toán mở khác nữa.
Bài toán vẫn chưa được giải. Tôi khẳng định như vậy bởi dạo gần đây có khá nhiều tuyên bố dễ gây nhầm lẫn về một chứng minh được đề xuất bởi Shinichi Mochizuki vẫn chưa được xác nhận từ năm 2012, và hiện tại chỉ có một số các nhà toán học tin rằng nó là một lời giải đúng đắn cho Giả thuyết ABC. Rất nhiều câu hỏi về giả thuyết này đã - được - hỏi - trên - Quora.

Image result for Thuyết bên trong Vũ trụ Teichmüller

Thêm chú thích

(Tình cảnh này thực sự là tôi buồn. Giả thuyết ABC là một thứ vô cùng đẹp đẽ, công trình nghiên cứu sâu sắc xung quanh nó thật sự thú vị và hấp dẫn. Nhưng công chúng chỉ bị hấp dẫn bởi drama, và drama ngăn cản bản chất thực sự của giả thuyết bộc lộ ra ngoài. Chưa có lý do gì để đáng bị kích động bởi chứng minh của Mochizuki. Chưa đâu, dù ở mức nào đi nữa.)
Sự phát triển của "Thuyết bên trong Vũ trụ Teichmüller", nếu khả thi, sẽ là một tiến triển đáng ghi nhận. Thay vào đó, tìm những cách khác để công phá Giả thuyết ABC và liên kết chặc chẽ với Giả thuyết Szpiro sẽ chắc chắn thỏa mãn điều kiện trở thành Bài toán Lớn.

xem thêm tại ca cuoc bong da:

Labels

Thứ Ba, 10 tháng 3, 2020

Bài toán lớn tiếp theo mà các nhà toán học đang cố gắng giải là gì?

Không có nhận xét nào:

Đăng nhận xét

Link hay

I Am The Author